In annuity schedules, the loan payment is the same every month, if the interest rate and its calculation periods remain unchanged. At the beginning of the loan agreement, the interest portion of the monthly payment is larger, and the principal portion is smaller. In time, their proportions change - the interest portion decreases, while the principal portion increases.
In the sample schedule, where the length of each month is normally calculated to be 30.42 days (365 days divided by 12 months), the annuity schedule would look like this:
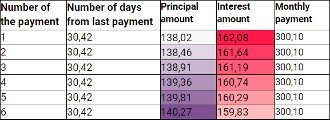
In the example, it is easy to see how the amount of the principal part increases every month and the interest part decreases every month.
There is not an equal number of days in each month, which means that real loan schedules will not change exactly according to the sample. In their loan schedule, the customer pays interest according to the actual number of days between two monthly payments. If the number of days between monthly payments is different, then the amount of interest in the next payment may not be lower than the previous one.
Let's imagine a situation where a customer was issued a loan amount on March 20, 2023, and he chose the 20th as his monthly payment date.
The beginning of a realistic loan schedule would look like this:
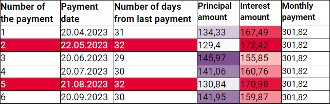
What does an annuity schedule that uses the actual number of days per month show?
- In the case of payment number 2, May 20th is a Saturday, therefore the payment will be moved to the following working day - May 22nd. The interest portion is higher in this payment compared to the previous month, because the number of days between two monthly payments is greater - the customer pays interest for 32 days, not 31 days (as for the first payment).
- The same situation occurs when comparing payments number 4 and 5.
- If the interest portion of the monthly payment increases (interest is paid for a longer period), it also changes the amount of the principal. In annuity schedules, the most important part is to keep the monthly payment amounts equal, and therefore, as the interest portion increases, the amount of the principal portion in the payment decreases.
Here is an example where the interest and principal payments over six months are added together:
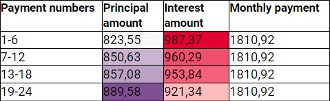
If you look at your loan schedule over longer periods, you can see that the actual schedule also moves according to the principle of the annuity schedule - over time, the interest portion decreases and the principal portion increases.


